Lesson 2: The Magic of Compounding
When should I start saving for retirement?
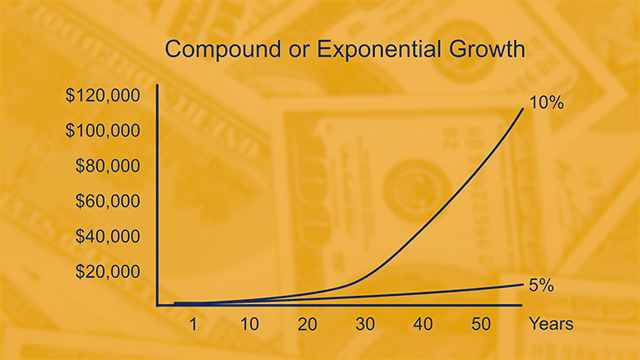
Compounding works in an amazing way. In Lesson 2, Professor Bartlett explains how a $1000 investment can grow exponentially as decades of returns pile up in your account.
Scroll down for some thought questions and case study examples or download discussion in a PDF file.
#1: What are the factors that would increase my initial investment over a period of time?
We need to consider the following three factors when investing over a period of time:
- The rate of return
- The initial amount invested and/or how much we contribute regularly
- The length of the investment period
The higher the rate of return, the more you contribute, and the longer the period of investment, the more your investment grows. The best decision you can make is to start to save and invest for your retirement early. If, for some reason, you cannot start saving right now, seriously consider increasing your future contributions.
#2: If I haven’t been contributing to a retirement fund in any significant way and I’ve missed out on 10 or 20 years of compound growth, is there any way to “catch up”?
No… and yes. You can never truly make up for missing out on those years of compound growth. However, if you have the means, you might be able to contribute more now than you would have in those earlier years. And if you start with $10,000 in an account that earns compound interest, the actual dollar amount of the account will grow much faster than if you only started with $1,000 (as in Professor Bartlett’s example). The main thing to understand is that the best time to start saving is RIGHT NOW.
#3: How do I know if an account is earning compound interest?
Ask! Most investment vehicles do earn compound interest, but it is always a wise move to ask lots of questions about an account before putting your money there. The more you understand, the more confident you can be that your money is in the right place.
#4: I contribute to my retirement fund, but sometimes I just feel like that money is going into a black hole. Is there some way to keep track of it better?
Of course! You should receive statements from whichever company is managing your retirement account (T. Rowe Price, TIAA Cref, Vanguard, etc.). These statements are often sent out on a quarterly basis, or you can receive them electronically. Almost all companies now allow you access to your account online as well. So, be proactive! Occasionally, take a moment to check out how much money you’ve been saving, but recognize that there will be short-term bumps and bubbles along the way to retirement. Since you won’t be spending the money until you retire, invest for the long-term!
#5: What is the Rule of 72?
The Rule of 72 is an easy way to approximate how many years it will take until some initial investment doubles in value. The number of years an investment will take to double can be approximated by dividing 72 by the average interest rate an account earns. Thus, an initial investment that earns 6% interest will double in value every 72/6 = 12 years. Keeping track of your finances in this way can be very empowering and inspiring!
Continuing example stories from three different stages in life.
Lesson 2: The Magic of Compounding
The greater the average rate of return, the more dramatic the power of compound interest. All of our Smithies want to take advantage of this effect.

Grace, recent graduate, 24
After watching the graphic of 10% growth compounded over 50 years, Grace really, really doesn’t want to give up that last decade of earnings. She is committed to setting up a retirement fund immediately, even if she can’t put much into it just yet.
After doing a few calculations, Grace figures that if she makes her lunch to take to school five days each week, she can save $83 per month, or $1000 per year. If she then puts $1000 every year into her retirement fund and earns a 6% return, the magic of compounding will make her account grow to $154,762 in forty years when she is ready to retire at age 64. And because after she retires Grace will withdraw money from her retirement fund gradually for the following two decades, her retirement fund will have even more time to grow.
Maybe she’ll also ask her parents to contribute to her retirement fund instead of buying her a Christmas present this year…

Sarah, entrepreneur, 39
Sarah is really glad that she and her partner have been contributing to their retirement funds for the past 7 or 8 years, since she knows they only have another 25 or 30 years until they will both be thinking seriously about retiring. She’d love to contribute more to those funds to take full advantage of the compound growth they produce, but she has too many other expenses on the horizon to do so right now.
First, they need to take care of their credit card debt so that compound growth is no longer working against them in the form of credit card interest, canceling out much of the growth of their retirement funds. Once their credit card debt is erased, compound growth will be acting only as their friend, instead of also acting as their enemy. Hopefully, they can contribute more to their retirement funds after paying off the credit card debt to at least partially offset the effect of the lost decade of saving.
Joanne, artist and activist, 66
Joanne and the phenomenon of compound growth have been good friends for many years now. Together they have built a very comfortable retirement fund for Joanne to use as she steps back from the world of work. Without such exponential growth, she would not have been able to retire yet, or perhaps even at all. It is a source of pride for Joanne that even in the leaner years, she always put away as much as she could into that “magical container.”
She remembers when her own grandmother died and left her $10,000 in her will 36 years ago, when Joanne was 30. Instead of spending the money, Joanne decided to save it and it has earned an average of 6% per year in a mix of stocks and bonds. Using the rule of 72, we can calculate the current value of that bequest. At 6% annual interest, it took 72/6 = 12 years to double in value, another 12 years to double again (at which point it was worth $40,000), and another 12 years to double yet once more. Consequently, her inheritance of $10,000 has doubled in value three times and is now worth (approximately) $80,000.
Joanne sends the link to this course to her children to encourage them to use the time still available to them to take advantage of the magic of compounding.